Các thuật toán xuất hiện ở khắp mọi nơi trong xây dựng và phát triển phần mềm. Cho dù bạn có để ý thấy chúng hay không, thì vai trò của các thuật toán là vô cùng quan trọng trong việc xây dựng, tối ưu, sửa lỗi các phần của một chương trình máy tính. Việc nắm vững các thuật toán sẽ giúp kỹ sư phần mềm hay lập trình viên xây dựng được những ứng dụng hoạt động hiệu quả, tối ưu công suất, phục vụ tốt nhất cho người dùng.
Trong thực tế có rất nhiều thuật toán khác nhau. Tuy nhiên chúng tôi tin rằng có một số thuật toán cơ bản mà lại cực kỳ hữu dụng với Software Engineers và Software Developers. Hãy cùng FSE tìm hiểu những thuật toán này nhé.
Thuật toán sắp xếp – Sorting Algorithms
Sắp xếp các tập dữ liệu thô là một bước đơn giản nhưng quan trọng trong khoa học máy tính/dữ liệu và ngày càng quan trọng trong thời đại Big Data. Sắp xếp thường liên quan đến việc tìm thứ tự số hoặc chữ cái (tăng dần hoặc giảm dần).
Insertion Sort
Thao tác này sắp xếp từng bước một mảng, tạo danh sách được sắp xếp bằng cách xem xét từng mục không có thứ tự và di chuyển nó vào một vị trí thích hợp. Nó thường được so sánh với cách chúng ta thường sắp xếp một bộ bài sau khi được chia ngẫu nhiên (ví dụ: di chuyển các số thấp hơn sang trái và vua/quân hậu sang phải cho đến khi chúng theo thứ tự tăng dần). Nó là một thuật toán nhanh và hiệu quả trên các tập dữ liệu nhỏ hơn.
Selection Sort
Đây là một biến thể ở trên. Với các loại lựa chọn, dữ liệu được chia thành hai phần ‘được sắp xếp’ và ‘không được sắp xếp’. Thuật toán quét phần chưa sắp xếp để tìm giá trị nhỏ nhất và di chuyển nó đến phần đã sắp xếp (ở bên trái danh sách). Sau đó, nó lặp lại quá trình này, dần dần xây dựng một mảng được sắp xếp theo thứ tự tăng dần. Một lần nữa, điều này phù hợp hơn cho các tập dữ liệu nhỏ.
Bubble Sort
Tính năng này hoạt động bằng cách quét qua mọi mục trong danh sách và hoán đổi các mục liền kề nếu chúng sai thứ tự. Quá trình được lặp lại cho đến khi không có phần tử nào trong danh sách bị bỏ sót. Ví dụ: trong một dãy số ngẫu nhiên mà bạn muốn sắp xếp theo thứ tự tăng dần, thuật toán sẽ chuyển qua dãy số đó nhiều lần cho đến khi tất cả các số khớp với dãy số đó. Như với insertion sort, điều này được sử dụng tốt nhất khi cấu trúc dữ liệu tương đối nhỏ hoặc đã được sắp xếp một phần, nếu không, nó có thể là một quá trình tốn thời gian.
Quick Sort
Đây được gọi là thuật toán ‘chia để trị’ vì thuật toán này liên tục chia nhỏ cấu trúc dữ liệu thành các danh sách con để giải quyết vấn đề sắp xếp. Trong trường hợp này, một phần tử trở thành ‘trục’ và tất cả các phần tử khác được phân vùng tùy theo chúng lớn hơn hay nhỏ hơn giá trị trục. Sau đó, quy trình được lặp lại trong các danh sách phụ này cho đến khi mỗi danh sách chỉ có một mặt hàng, lúc đó toàn bộ chuỗi sẽ được sắp xếp.
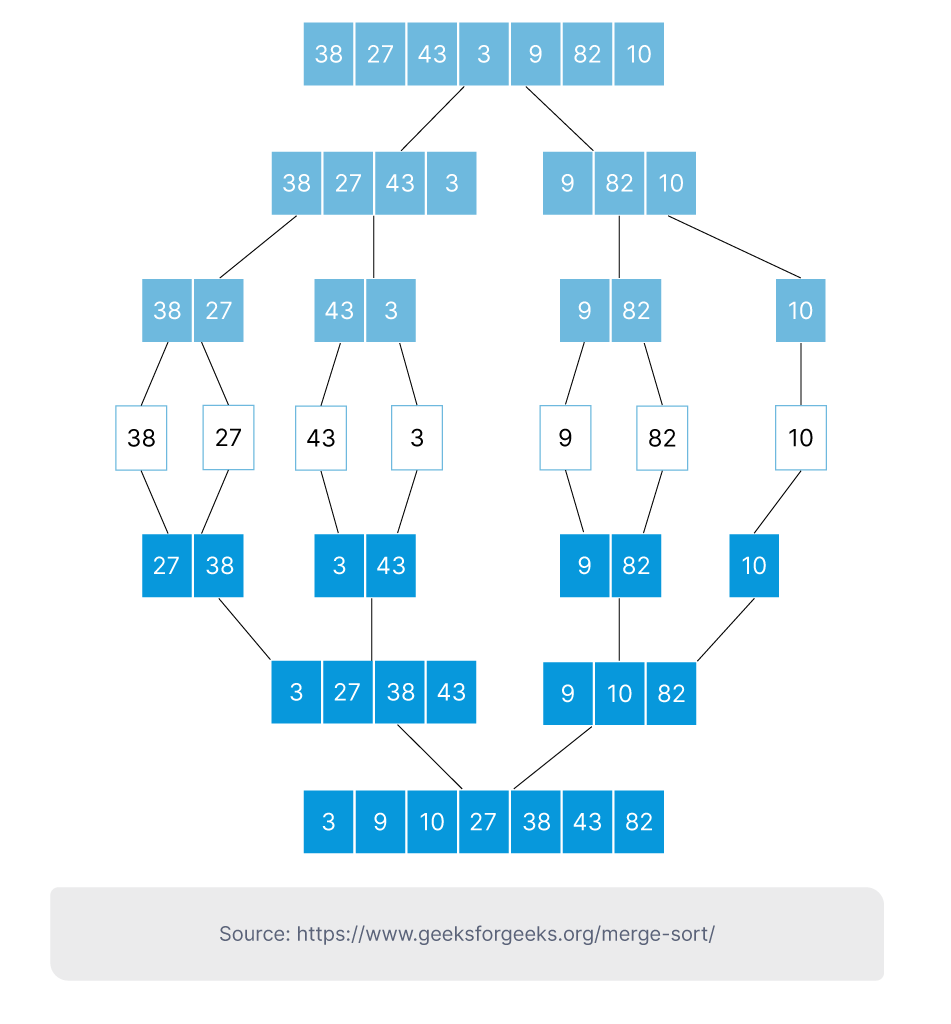
Merge Sort
Đây là một hướng dẫn phân chia và chinh phục khác liên tục chia cấu trúc dữ liệu thành hai nửa cho đến khi mỗi danh sách con chỉ có một hoặc hai mục. Sau đó, chúng được đặt theo thứ tự cần thiết và cuối cùng, tất cả các danh sách phụ được hợp nhất với nhau theo đúng thứ tự.
Thuật toán tìm kiếm – Searching Algorithms
Tìm kiếm là một chức năng cơ bản, nhưng rất quan trọng và cần phải thực hiện đúng khi lập trình. Nó có thể liên quan đến việc tìm kiếm thứ gì đó trong cơ sở dữ liệu nội bộ hoặc truy tìm không gian ảo để tìm một phần thông tin cụ thể và có hai cách tiếp cận tiêu chuẩn được sử dụng ngày nay.
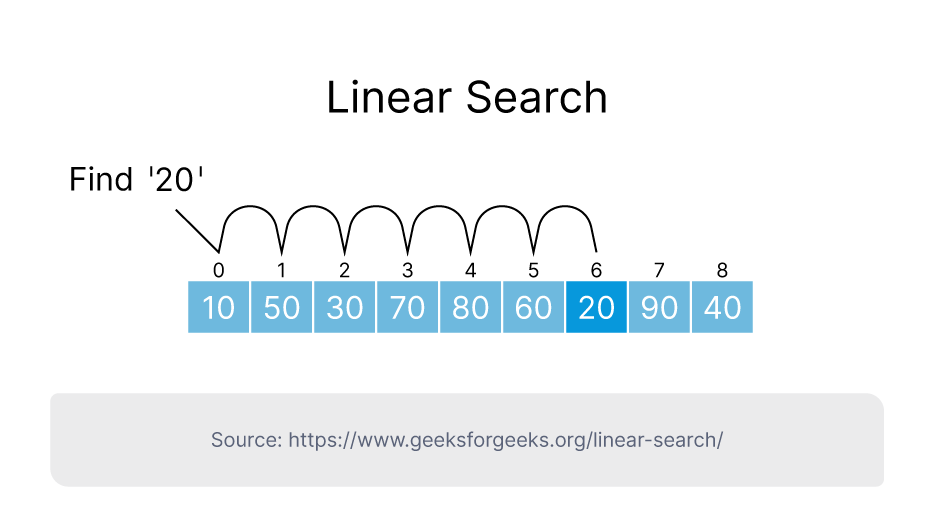
Linear Search
Đây là một thuật toán đơn giản được sử dụng để tìm một phần tử hoặc một phần thông tin cụ thể trong một tập dữ liệu chưa được sắp xếp. Nó sử dụng một định dạng tìm kiếm tuần tự. Ví dụ: nếu bạn cần truy xuất một số điện thoại di động từ cơ sở dữ liệu khổng lồ gồm những người ngẫu nhiên, thuật toán tìm kiếm tuyến tính sẽ tuần tự đi qua từng số cho đến khi tìm thấy mục có liên quan.
Binary Search
Điều này sử dụng một cách tiếp cận khác, tìm kiếm cấu trúc dữ liệu theo khoảng thời gian thay vì tuần tự. Nó có thể là một phương pháp hiệu quả hơn khi được sử dụng trên các cấu trúc dữ liệu mảng được sắp xếp, vì không cần phải quét toàn bộ chuỗi.
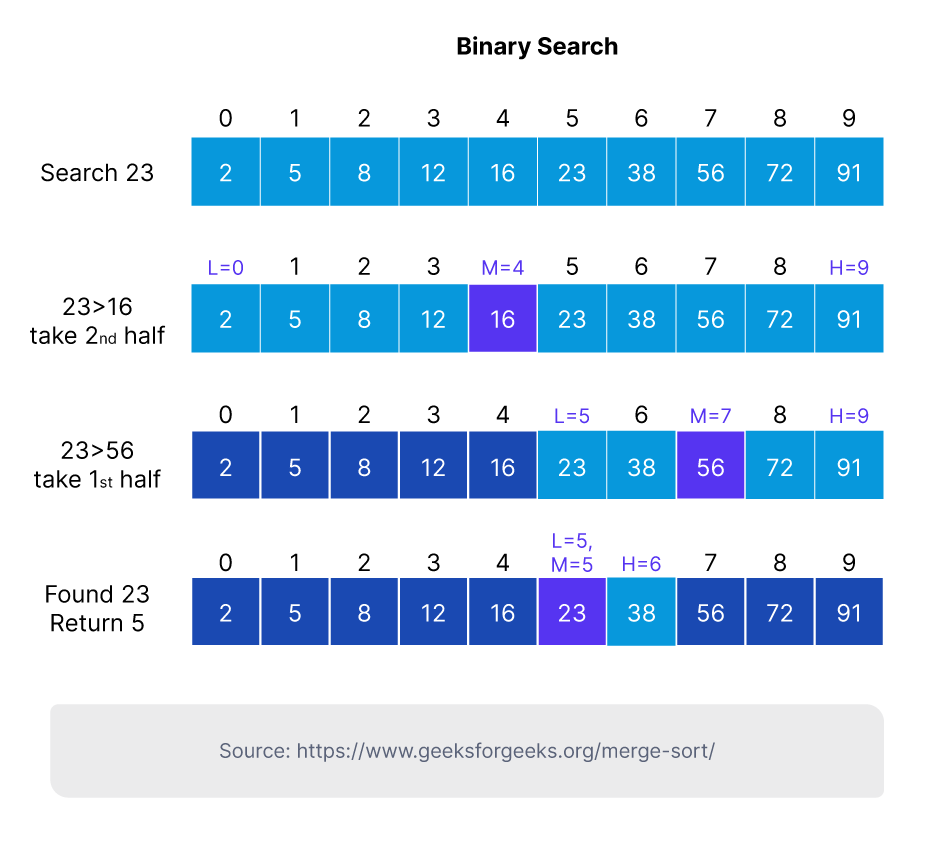
Ví dụ: trong một chuỗi dài các số tăng dần, tìm kiếm nhị phân sẽ bắt đầu với phần tử ở giữa – nếu phần tử này không khớp và nằm dưới số được yêu cầu, thì nó sẽ tìm mục ở giữa của nửa danh sách phía trên điểm đó ( nếu mục ở giữa cao hơn số lượng yêu cầu, nó sẽ tìm kiếm một nửa bên dưới điểm này). Quá trình này sẽ tiếp tục cho đến khi nó tìm thấy mục hoặc không còn danh sách phụ nào, nghĩa là mục tiêu không có ở đó.
Thuật toán đồ thị – Graph Algorithms
Đồ thị là một công cụ quan trọng trong trực quan hóa dữ liệu, thường được sử dụng để biểu thị các mục dữ liệu dưới dạng các ‘nút’ (node) được kết nối với nhau trong mạng. Các nút này có thể đại diện cho từng người dùng của nền tảng truyền thông xã hội hoặc các địa điểm trong thành phố. Về cơ bản, nếu bạn có một tập hợp các đối tượng có liên quan với nhau, thì rất có thể bạn có thể biểu diễn chúng bằng biểu đồ.
Breadth-First Search (BFS)
Công cụ này được sử dụng để duyệt qua cấu trúc cây hoặc biểu đồ bằng cách bắt đầu từ một ‘gốc’ duy nhất và khám phá tất cả các nút lân cận. Sau đó, nó sẽ chuyển sang nút gần nhất tiếp theo chưa được khám phá và lặp lại quy trình ở cấp độ tiếp theo, tiếp tục theo cách này cho đến khi tất cả các nút đã được phân tích. Đây là một phương pháp hữu ích để tìm đường đi ngắn nhất qua các nút của cấu trúc đồ thị.
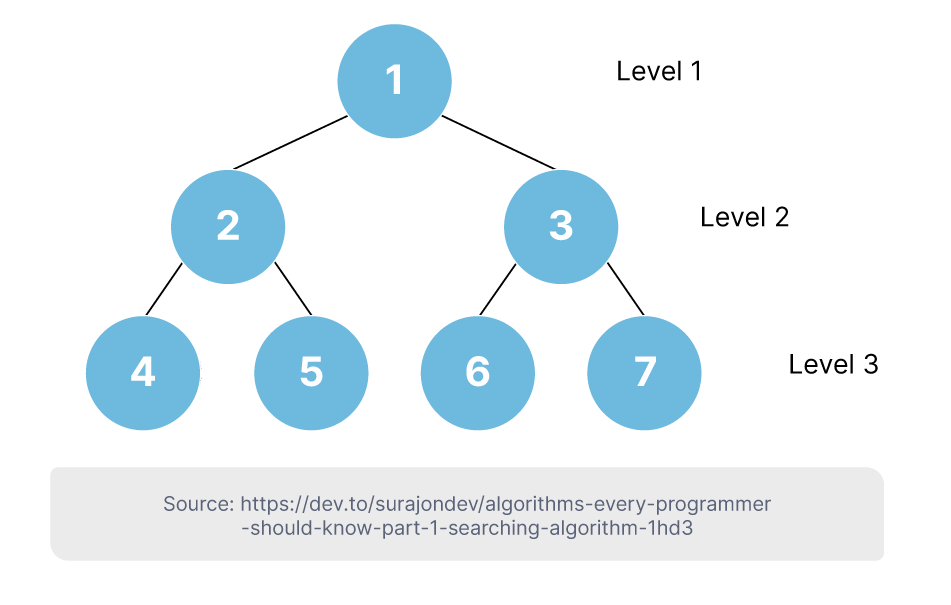
Depth-First Search (DFS)
Thay vì rải ra từng lớp từ gốc như với BFS, thuật toán DFS sẽ chọn một nút gốc và sau đó khám phá càng xa càng tốt dọc theo một nhánh dẫn từ nút đó (và tất cả nhánh phụ của nó). Sau đó, nó quay trở lại dọc theo nhánh về gốc và bắt đầu lại quá trình dọc theo nhánh khác. Nó thường là một lựa chọn phù hợp hơn khi nút đích cách xa nguồn.
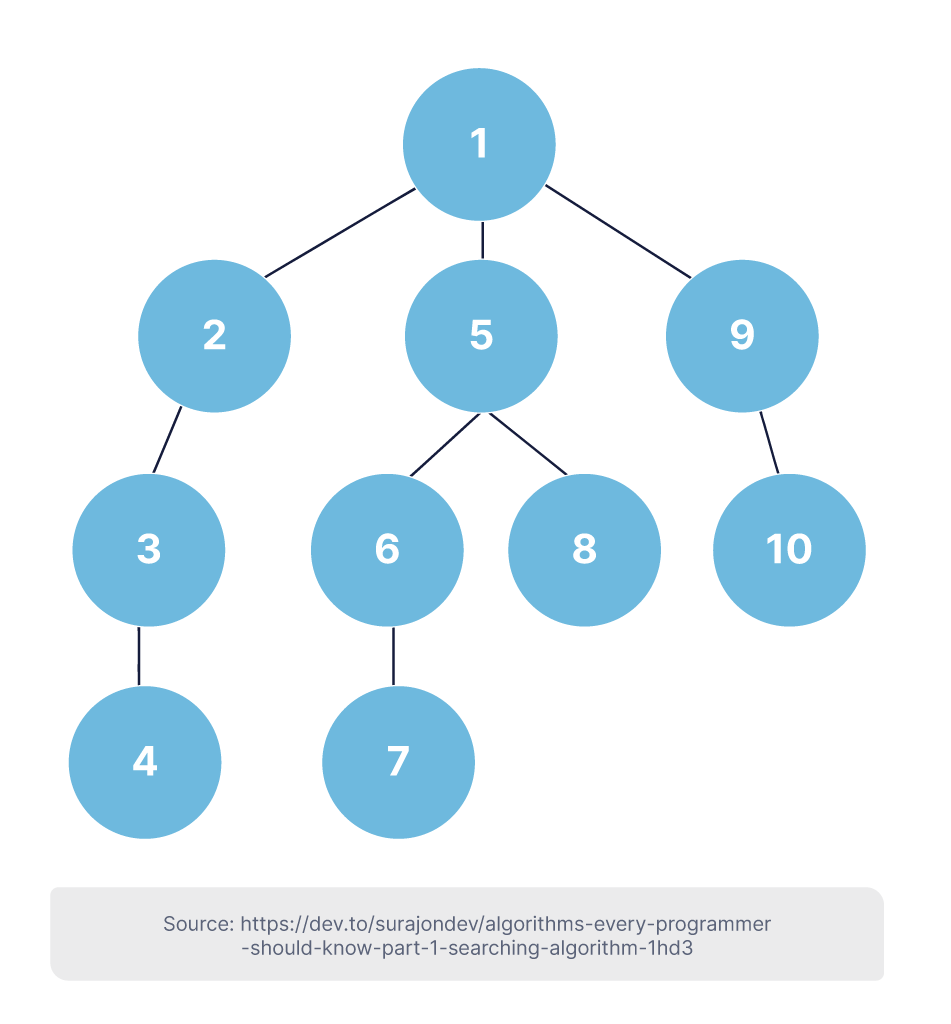
Dijkstra (Shortest Path)
Tính năng này tìm đường đi ngắn nhất giữa các nút trong cấu trúc biểu đồ. Thuật toán, được đặt theo tên của nhà khoa học máy tính người Hà Lan Edsger W. Dijkstra, ánh xạ một cây các đường đi ngắn nhất từ nút bắt đầu tới mọi nút được kết nối khác. Có lẽ ứng dụng nổi tiếng nhất của thuật toán này là với bản đồ của Google, tính toán nhanh tuyến đường nhanh nhất giữa hai điểm bất kỳ trên bản đồ (và cập nhật điều này liên tục).
Kruskal/Prim
Đây là hai thuật toán ‘tham lam’ được sử dụng để tìm cây bao trùm tối thiểu (MST) của cấu trúc đồ thị có trọng số. MST có nghĩa là trọng số tối thiểu của các cạnh được sử dụng để kết nối tất cả các nút (hoặc đỉnh) trong cấu trúc đồ thị. Thuật toán Kruskal thêm các cạnh có trọng số thấp nhất trong một cấu trúc cho đến khi chúng kết nối với nhau để tạo thành một MST. Thuật toán Prim tìm MST bằng cách bắt đầu với một đỉnh ngẫu nhiên và xây dựng đến đỉnh tiếp theo thông qua các cạnh có trọng số thấp nhất.
Một số thuật toán khác
Hashing
Điều này ngày càng phổ biến khi chúng ta xử lý các cấu trúc dữ liệu ở quy mô không thể tưởng tượng được trước đây và ngày càng quan tâm đến vấn đề bảo mật. Băm chuyển đổi dữ liệu có độ dài tùy ý thành độ dài cố định (“giá trị băm”), dữ liệu này cung cấp bản tóm tắt ngắn hơn về dữ liệu gốc. Một cách sử dụng phổ biến cho các bảng băm là mã hóa các khóa hoặc tin nhắn.
Randomized
Các thuật toán này nhất thiết phải bao gồm một mức độ ngẫu nhiên như một phần logic của chúng và thường được sử dụng với khối lượng dữ liệu lớn khó xử lý. Yếu tố ngẫu nhiên có thể là thời gian dự kiến cần thiết để tìm ra giải pháp chính xác (ví dụ: Las Vegas) hoặc xác suất mà một kết quả cụ thể là chính xác sau khi chạy thuật toán trong một khoảng thời gian nhất định (ví dụ: Monte Carlo).
Tham khảo: Geeksforgeeks, Jobsity